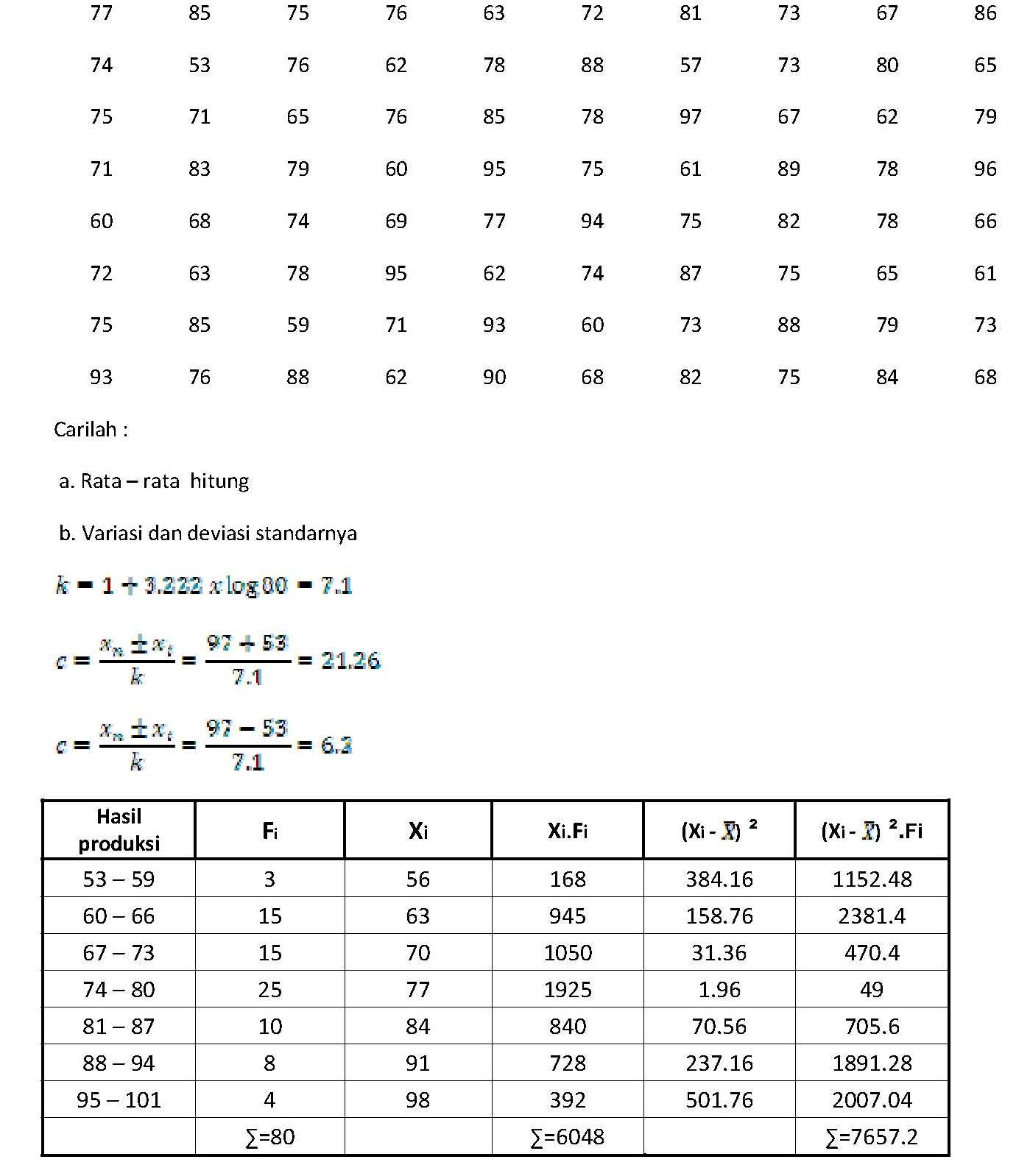
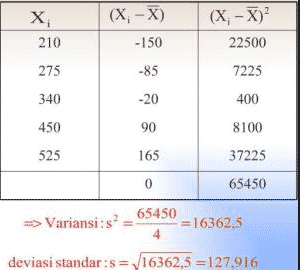
Berdasarkan pengambilan sampel nilai ujian mata pelajaran beberapa siswa di smp bahagia diketahui data sebagai berikut. Berikut ini ada beberapa contoh soalnya yang diantaranya sebagai berikut.

Sampling Analisis
Contoh soal standar deviasi. Contoh soal standar deviasi diketahui data nilai matematika 10 siswa kelas 2 sma 1 purbalingga adalah. 84 86 89 92 82 86 89 92 80 86 87 90. 84 86 89 92 82 86 89 92 80 86 87 90. Data umur berbunga atau hari dari tanaman padi varietas dan pandan wangi ialah. Berapakahkah standar deviasi dari data yang di atas. 80 60 80 90 70 80 95.
Standar deviasi menyatakan keragaman sampel dan dapat digunakan untuk mendapatkan data dari suatu populasi. Standar deviasi adalah nilai yang menggambarkan seberapa besar perbedaan antar data hasil pengukuran atau persebaran datanya terhadap nilai rata rata. Berikut ini terdapat beberapa contoh soal dari standar deviasi terdiri atas. Dalam bahasa inggris standar deviasi disebut standard deviation. Data umur berbunga hari tanaman padi varietas pandan wangi adalah sbb. Standar deviasi di dalam sampel nilai ujian kita dengan demikian adalah 219.
Standar deviasi juga disebut simpangan baku dan disimbolkan dengan alfabet yunani sigma σ atau huruf latin s. Biasanya paling tidak 68 dari semua sampel akan jatuh di dalam salah satu standar deviasi dari mean. Mengitung standar deviasi simpangan baku contoh soal selama 10x ula berturut turut ulangan semester di kampus tercintanya di london jonathan mendapat nilai 91 79 86 80 75 100 87 93 90dan 88. Data umur berbunga hari tanaman padi varietas pandan wangi adalah sbb. Sebagai contoh silahkan lihat contoh di bawah ini. Ingatlah bahwa di dalam sampel nilai ujian variannya adalah 48.
Contoh soal standar deviasi. Nilai ini adalah nilai standar deviasi. Rumus standar deviasi di excel adalah stdev. Berapakah standar deviasi dari data di atas. Hitunglah nilai standar deviasi dari data tersebut. Berikut ini terdapat beberapa contoh dari standar deviasi diantaranya.
Pengertian rumus dan contoh soal standar deviasi a. 84 86 89 92 82 86 89 92 80 86 87 90. Semakin besar persebaran datanya maka nilai standar deviasinya juga semakin besar. Contoh soal nah setelah anda mengetahui rumus atau cara menghitung simpangan baku maka anda bisa melihat beberapa contoh soal serta pembahasannya berikut ini. Agar anda lebih memahami metode standar deviasi ini.